Mô hình hóa trường nhiệt độ và trường ẩm trong khuôn cát tươi

Bài báo này tập trung xây dựng mô hình cho bài toán nhiệt và ẩm trong khuôn dựa vào nguyên lý truyền nhiệt trong hệ vật liệu xốp và bài toán chế độ khí trong khuôn…

Modeling of temperature and moisture fields in green sand molding

Trần Xuân Tiến, Đào Hồng Bách
Viện Khoa học và kỹ thuật vật liệu, Trường Đại học Bách khoa Hà Nội

Ngày nhận bài: 15/7/2015, Ngày duyệt đăng: 28/7/2015

TÓM TẮT

Đã thiết lập một mô hình toán dùng để tính và mô phỏng trường nhiệt độ và trường ẩm trong khuôn cát tươi. Mô hình cho phép tính đồng thời sự phân bố nhiệt và ẩm trong khuôn, kết quả mô phỏng đường cong nhiệt trong khuôn khá tương đồng với nghiên cứu thực nghiệm. Kết quả thu được có ý nghĩa rất quan trọng trong quá trình mô hình hóa, mô phỏng số quá trình đúc trong khuôn tươi, do đó có thể điều khiển quá trình đông đặc cũng như khống chế ảnh hưởng của độ ẩm đến chất lượng vật đúc.

Từ khóa: phân bố ẩm, phân bố nhiệt độ, khuôn cát tươi, mặt hóa hơi, mặt ngưng tụ.

ABSTRACT

The paper presents a mathematical model established to calculate and to simulate the temperature-moisture field in the green-sand mold. The model enables simultaneous calculation of heat and moisture distribution in the mold. The numerical results obtained for the temperature curves in the green-sand mold are in good agreement with experimental data. This result is very important in modeling and simulating the casting process in the green- sand mold. Thus, one can control the solidification process and moisture affect on the casting quality.

Keywords: moisture and temperature distributions, green sand mold, vaporization and condenzation fronts.

1. ĐẶT VẤN ĐỀ

Hiện nay, việc hoàn thiện công nghệ đúc trong khuôn có chứa nước như khuôn CO₂ và khuôn tươi cát-sét là hướng được tập trung nghiên cứu trên thế giới, bởi đây vẫn là một công nghệ đúc chính trong công nghiệp, đặc biệt đối với các sản phẩm đúc gang và thép [1]. Do đó, việc hiểu rõ các quá trình nhiệt và ẩm trong khuôn, từ đó điều khiển quá trình đông đặc nhằm nâng cao chất lượng vật đúc, hiệu quả sản xuất, đồng thời góp phần tối ưu dây chuyền đúc tự động có vai trò đặc biệt quan trọng và rất cấp thiết. Để làm điều đó ta cần mô hình hóa trường nhiệt độ và trường ẩm trong khuôn.

Do có chứa nước nên trường nhiệt trong khuôn diễn ra phức tạp hơn khi có sự chuyển pha của nước (quá trình bay hơi ở vùng nhiệt độ cao, ngưng tụ ở nơi nhiệt độ thấp), nó làm cho việc mô hình hóa bài toán nhiệt và ẩm gặp nhiều khó khăn. Các công trình nghiên cứu về trường nhiệt và trường ẩm của các tác giả Veinik [2], Lê Công Kha [3] đã đưa ra mô hình trường nhiệt của khuôn, xây dựng trường nhiệt dựa vào thực nghiệm. Các công trình của Tsai et al. [4], Shih et al. [5], Hsiau et al. [6] đã đưa ra mô hình toán cho trường nhiệt độ khuôn thông qua trường nhiệt độ vùng cát khô. Công trình của A.C. Cavinov [7] đã nghiên cứu về trường nhiệt bằng sai phân mạng hiện, còn trường ẩm dựa vào nghiên cứu thực nghiệm. Các công trình này cơ bản đã đưa ra mô hình cho bài toán nhiệt trong khuôn tươi, có tính đến sự bay hơi của nước, tuy nhiên với mô hình đó thì trường ẩm trong khuôn chưa được đề cập đến, bởi mô hình mới chỉ tính đến vùng nhiệt độ từ 373 K (100^oC) trở lên, vùng nhiệt độ dưới 373 K (100^oC) nơi có sự bay hơi và ngưng tụ vẫn chưa được quan tâm.

Trong công trình của Kubo et al và Penhlke et al. [1] đã đề cập đến việc mô hình hóa bài toán nhiệt và ẩm trong khuôn cát tươi bằng các phương trình toán, tuy nhiên tác giả không đi sâu vào giải quyết mô hình mà lại đề xuất một phương án tính toán gần đúng bằng phương pháp Neumans.

Bài báo này tập trung xây dựng mô hình cho bài toán nhiệt và ẩm trong khuôn dựa vào nguyên lý truyền nhiệt trong hệ vật liệu xốp và bài toán chế độ khí trong khuôn.

2. CÁC QUÁ TRÌNH LÝ HÓA TRONG KHUÔN

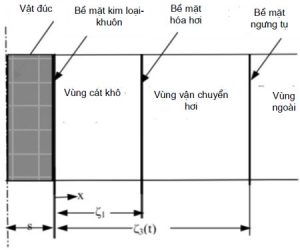
Khi rót kim loại lỏng vào khuôn cát tươi, dưới tác dụng của nhiệt kim loại lỏng, tại bề mặt tiếp xúc với khuôn đúc hơi nước bị bay hơi nhanh chóng và tạo thành gradient áp suất trong khuôn và các vùng đặc trưng trong khuôn. Trong vùng nóng của khuôn, áp suất của hơi nước bão hòa cao hơn so với trong vùng lạnh. Khi luân chuyển theo vòng tròn thì ở lớp dọc trục đưa một cách liên tục khí có lượng ẩm tăng từ vùng nóng sang vùng lạnh, còn ở lớp biên đưa khí có lượng ẩm thấp từ vùng lạnh sang vùng nóng. Như vậy trong vùng nóng hơi nước có áp suất nhỏ hơn áp suất bão hòa, còn trong vùng lạnh thì có áp suất lớn hơn áp suất hơi bão hòa (hình 2).

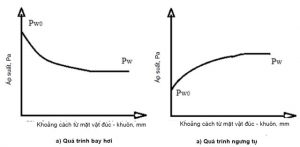
Tỷ phần bay hơi và ngưng tụ được tính theo công thức sau [6]:

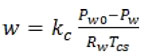
Trong đó: T_cs – nhiệt độ khuôn; P_w0 và P_w tương ứng là áp suất hơi bão hòa và áp suất riêng phần hơi nước tại nhiệt độ T_cs; k_c là hệ số truyền khối của hơi nước ứng với điều kiện bay hơi và ngưng tụ.

Hệ số truyền khối kc được tính theo bài toán dòng thông qua các chỉ số Reynolds và Schmidt như sau:

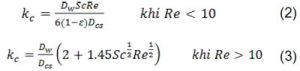
Trong đó: D_w – hệ số khuếch tán hơi nước (m²/s); S_c – số Schmidt v/D_w; v – độ nhớt động học của khí (m²/s); D_cs – đường kính trung bình của hạt cát-sét, (m); Re – số Reynold u.D_cs/v; ε – độ xốp của khuôn.

Hỗn hợp khí trong khuôn (hơi nước+không khí) ngoài việc tuân theo định luật thấm, còn di chuyển trong khuôn bằng cơ chế khuếch tán:

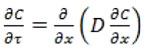
Trong đó: C – là nồng độ hơi nước trong khuôn (kg.mol/m³); D – hệ số khuếch tán hơi nước (m²/s), hệ số khuếch tán của hơi nước được xác định trong đó D₀ = 2,76 (m²/s).

3. MÔ HÌNH TOÁN VÀ PHƯƠNG PHÁP SỐ

Xét mô hình khuôn gồm các phần tử sau: các hạt cát-sét và khí trong khuôn (giả thiết khí ở đây chỉ gồm không khí và hơi nước).

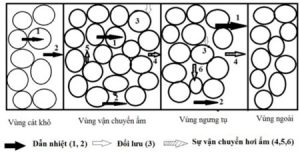
Dựa trên phân tích trong về quá trình nhiệt trong khuôn, theo lý thuyết truyền dẫn tổng quát [8] thì quá trình dẫn nhiệt chính trong khuôn gồm có quá trình truyền nhiệt dẫn nhiệt, quá trình dẫn nhiệt đối lưu. Sự dẫn nhiệt bao gồm sự dẫn nhiệt qua cát (hình 3(1)) và qua khí (hình 3 (2)). Sự truyền nhiệt đối lưu bao gồm sự truyền nhiệt bởi dòng khí, giữa cát và khí (hình 3 (3)). Sự truyền ẩm bao gồm dòng ẩm do sự chênh áp và khuếch tán (hình 3 (4)), dòng hóa hơi (hình 3 (5)) và dòng ngưng tụ (hình 3 (6)).

3.1. Mô hình toán bài toán nhiệt

Phương trình cân bằng năng lượng của hạt cát sét trong một đơn vị thời gian được viết như sau:

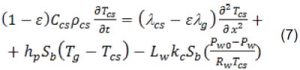
Phương trình cân bằng năng lượng của dòng khí trong khuôn là:

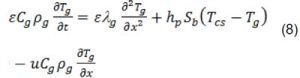
Trong đó: C_cs và C_g tương ứng là nhiệt dung riêng của khuôn cát-sét và hỗn hợp khí, J.kg/K; ρ_cs và ρ_g – lần lượt là khối lượng riêng của khuôn và của hỗn hợp khí trong khuôn, kg/m³; λ_cs và λ_g – độ dẫn nhiệt của khuôn và của hỗn hợp khí, (W/m.K); S_p – diện tích bề mặt riêng trên một đơn vị thể tích, (m²/m³); L_w – ẩn nhiệt hóa hơi của nước, (kJ/kg); R_w – hằng số khí của hơi nước, Pa.m³/(kg.K); T_g – nhiệt độ hỗn hợp khí trong khuôn; k_c – hệ số truyền khối được tính theo tiêu chuẩn Reynold và Nussel [6] theo công thức (2) và (3); hp – hệ số trao đổi nhiệt đối lưu của không khí với cát-sét được tính qua tiêu chuẩn Prandtl và Reynold như sau [9]:

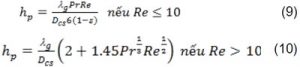
3.2. Mô hình bài toán truyền khối

Khi có sự tương tác giữa kim loại nóng chảy với bề mặt khuôn, thì tại mặt phân cách của khuôn với vật đúc sinh ra một áp suất dư so với áp suất khí quyền. Sự chênh áp đó tạo thành động lực đẩy chất khí trong khuôn ra xa so với bề mặt vật đúc, chất khí trong khuôn di chuyển với tốc độ u được xác định theo định luật Darcy như sau:

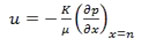
Trong đó: K – độ thấm theo định luật Darcy (m²); μ – độ nhớt của khí trong khuôn (Pa.s).

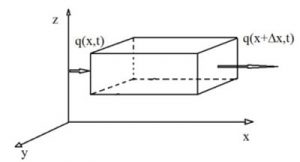
Theo [10] phương trình bảo toàn khối lượng của dòng khí khi đi qua một đơn vị thể tích (hình hộp chữ nhật) được viết như sau:

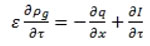
Trong đó: ρ_g – là mật độ khí; q – dòng khí trong

khuôn được tính theo công thức thấm khí p = ρ_gu; I – khối lượng riêng phần của chất khí, thoát ra từ một đơn vị thể tích hỗn hợp (do sự bay hơi của khí trong khuôn); ∂Ι / ∂τ – là công suất nguồn sinh khí, k_cS_b (P_w0). Giả thiết hỗn hợp khí chỉ gồm hơi nước và không khí khô, theo định luật Dalton với khí lý tưởng ta có phương trình sau:

P = P_w + P_a (13)

Trong đó: P_w và P_a tương ứng là áp suất riêng phần của hơi nước và không khí ở cùng nhiệt độ T.

Thay thế các công thức tính q và g vào biểu thức (12) và biến đổi ta nhận được hệ phương trình áp suất đặc trưng cho quá trình truyền khối trong khuôn như sau:

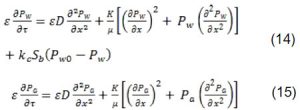
Từ phương trình bay hơi và ngưng tụ của hơi nước (1) ta tính được lượng ẩm theo phương trình sau:

3.3. Phương pháp giải

a) Điều kiện ban đầu

D_cs = 0,0002 mm, W₀ = 4 %, T₀ = 300 K, T_vđ  = T_rot = 933 K, ρ_cs = 1490 (2260) kg/m³, C_cs = 1134 J Kg/K, λ_cs  = 0,482 W/(mK), μ = 2,19*10^-7 Pa.s, λ_g = 0,0317 W/(mK), L_w = 3,14*103 – 2,34*T_cs kJ/kg, D_w = D_a = D = 2,28*10^-3*(Tg/273)1,78 m²/s, h_ngoai  = 20,8 W/m²K, C_a = 1,005 kJ/(kg.K), C_w = 1,846 kJ/(kg.K).

b) Điều kiện biên

Nhiệt độ:

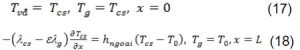
Điều kiện biên áp suất:

c) Mô hình sai phân khuôn

Khuôn dùng mô phỏng có chiều dày L = 100 mm, được chia thành 100 đoạn bằng nhau x = 1 mm; bước sai phân thời gian Δt = 0,002 s.

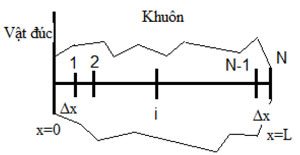
Sơ đồ giải thuật:

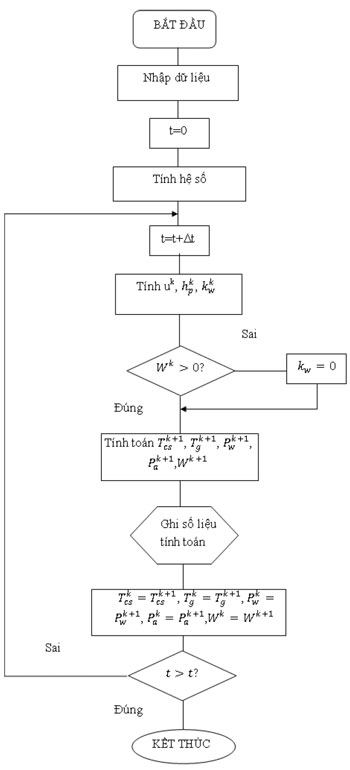
4. KẾT QUẢ VÀ THẢO LUẬN

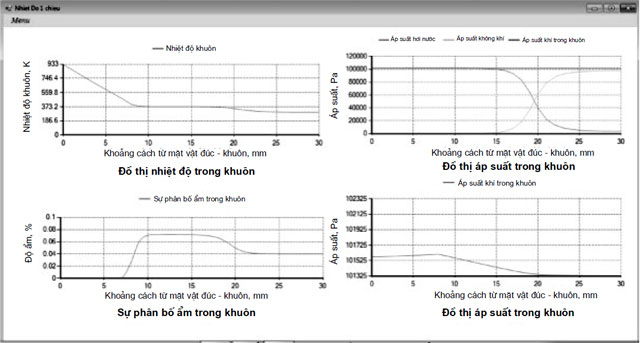
4.1. Sự phân bố nhiệt độ trong khuôn

Hình 7 mô tả sự phân bố nhiệt trong khuôn ở các vị trí khác nhau so với bề mặt tiếp xúc với vật đúc.

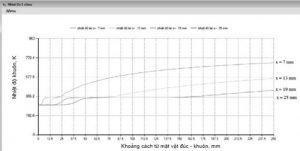
Nhiệt độ khuôn tăng dần từ nhiệt độ thường 300K (27 ^oC) đến 373 K (100 ^oC), sau đó giữ không đổi ở khoảng nhiệt độ này, đây là giai đoạn có sự ảnh hưởng của ẩn nhiệt bay hơi (ngưng tụ) của nước thể hiện là phần tử thứ 3 của vế phải phương trình nhiệt độ cát. Quá trình bay hơi (ngưng tụ) của nước làm nhiệt độ giữ không đổi do phần lớn lượng nhiệt được cấp cho quá trình bay hơi (ngưng tụ) của nước. Khi nước đã bay hơi hoàn toàn thì nhiệt độ của khuôn bắt đầu tăng dần theo thời gian.

Trường nhiệt độ trong khuôn tính bằng phương pháp số có kết quả tương đồng so với kết quả thực nghiệm (hình 8).

So với kết quả thực nghiệm thì nhiệt độ tính toán và thực nghiệm sai khác khoảng 5-8% giá trị ở các vị trí đo. Sự sai khác này chính là do sai số khi xác đinh khoảng cách bề mặt đến các vị trí đặt cặp nhiệt; độ trễ của tín hiệu nhận được khi đo do trong thực tế quá trình bay hơi ngưng tụ ở trong khuôn dễ dàng hơn trên các cặp nhiệt. Sai khác nhiệt độ giữa tính toán và thực nghiệm còn do độ chính xác của các giá trị nhiệt lý sử dụng trong tính toán.

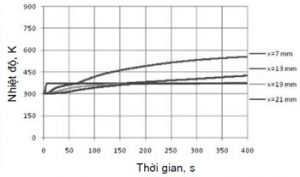
Để tăng độ chính xác của phép tính giảm sai số tính toán, ta có thể thực hiện bằng cách giảm sai số khi xác định các thông số nhiệt lý của khuôn.

4.2. So sánh vị trí mặt bay hơi giữa tính toán mô phỏng với thực nghiệm

Vị trí mặt hóa hơi theo thời gian sau khi rót trong khuôn được trình bày trên hình 9. Vị trí mặt hóa hơi xác định bằng tính toán xuất hiện nhanh hơn so với vị trí mặt hóa hơi tính bằng thực nghiệm [11].

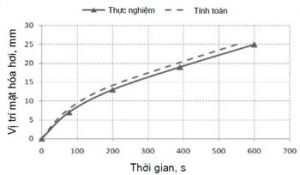
Sự sai khác của vị trí mặt hóa hơi giữa tính bằng phương pháp số và thực nghiệm là do sai khác về nhiệt độ phân bố ở các vị trí trong khuôn.

4.2. Trường nhiệt, trường ẩm và trường áp suất trong khuôn

Kết quả tính toán phân bố nhiệt, độ ẩm và áp suất trong khuôn được trình bày trên hình 10. Từ đồ thị ta thấy rõ các vùng đặc trưng trong khuôn, ứng với độ ẩm và áp suất cho từng vùng.

Vùng cát khô là vùng có nhiệt độ trên 373 K, độ ẩm là bằng 0; vùng vận chuyển ẩm là vùng ở khoảng nhiệt độ khoảng 368 đến 373 K, độ ẩm ở vùng này đạt giá trị lớn nhất 0,07%; vùng ngưng tụ là vùng nằm trong khoảng nhiệt độ từ 300 K đến 368 K, tương ứng với độ ẩm trong khoảng từ giá trị ẩm ban đầu W₀ = 0,04 đến giá trị ẩm lớn nhất 0,07. Từ hình vẽ ta có thể nhận ra ngay rằng vùng vận chuyển khí là vùng có sự chênh áp với vùng ngoài, sự chênh áp này là động lực cùng với sự khuếch tán làm cho khí di chuyển trong khuôn.

Trường nhiệt độ và trường ẩm trong khuôn phụ thuộc nhiều yếu tố [11], trong đó độ ẩm ban đầu có ảnh hưởng mạnh và rõ rệt nhất. Hình 12 mô tả sự phân bố ẩm trong khuôn với giá trị W₀ khác nhau. Từ hình vẽ ta thấy rằng độ rộng của vùng cát khô giảm dần khi độ ẩm ban đầu tăng nghĩa là tốc độ mở rộng vùng cát khô ở những hỗn hợp có độ ẩm lớn chậm hơn so với những hỗn hợp có độ ẩm thấp hơn.

Trong các tài liệu nghiên cứu trường nhiệt độ thông qua trường nhiệt vùng cát khô, độ ẩm lớn nhất được tính theo công thức sau:

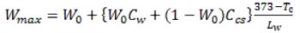
Bảng 1. So sánh giá trị độ ẩm lớn nhất giữa mô hình và công thức thực nghiệm

Độ ẩm, %	Tính theo công thức (21)	Tính theo mô hình	Sai số, %
2	0,05	0,054	8
4	0,07	0,076	8
7	0,10	0,109	9

So với giá trị tính theo công thức thực nghiệm (21) thì độ ẩm tính toán theo mô hình cao hơn, điều này là do nước không chỉ bay hơi ở vùng giữa vùng cát khô và vận chuyển ẩm mà nó còn bay hơi ngay trong vùng vận chuyển và vùng ngưng tụ, đồng thời trong thực tế khi hơi nước trong vùng vận chuyển không chỉ di chuyển theo hướng ra xa bề mặt phân cách vật đúc-khuôn mà còn có một phần hơi nước thoát lên trên điều này trong mô hình toán chưa tính đến. Tuy nhiên, với sai số đó không ảnh hưởng quá lớn đến bản chất và ý nghĩa của bài toán.

5. KẾT LUẬN

Công trình đã chỉ ra các quá trình đặc trưng trong khuôn cát tươi khi nung trong quá trình đúc, trên cơ sở đó thiết lập mô hình toán cho hai thông số đặc trưng bài toán truyền nhiệt và bài toán truyền khối cho bài toán một chiêu. Sử dụng phương pháp sai phân mạng hiện kết hợp với sai phân mạng ẩn trong giải bài toán nhiệt, ẩm và đạt kết quả sau:

1) Mô hình hóa được bài toán truyền nhiệt và truyền ẩm bằng các phương trình toán học cơ bản. Sự phân bố nhiệt trong khuôn bằng cách giải phương trình theo phương pháp sai phân cho kết quả tương đồng với các kết quả nghiên cứu trước đây.

2) Mô hình hóa được bài toán ẩm, kết quả tính toán cho phép xác định được sự phân bố độ ẩm trong khuôn theo từng thời điểm tính toán. Độ ẩm lớn nhất trong vùng vận chuyển có giá trị khá tương đồng so với công thức (21).

Để cho việc mô hình hóa đạt hiệu quả hơn trong thực tế, ta cần nghiên cứu ảnh hưởng của trọng trường đến quá trình nhiệt-ẩm trong khuôn, trên cơ sở đó tiến hành giải bài toán hai chiều có ảnh hưởng của trọng trường sẽ là vấn đề nghiên cứu tiếp sau.

Kết quả nghiên cứu này là cơ sở tiến tới mô hình hóa sự phân bố nhiệt độ và vị trí trường ẩm trong khuôn bằng mô hình toán học, đồng thời là cơ sở để xác định các điều kiện biên cho bài toán mô phỏng hóa trường độ và trường ẩm trong hệ khuôn có chứa nước, góp phần nâng cao chất lượng vật đúc.

Tài liệu tham khảo:

1. K. Kubo and R. D. Pehlke, Heat and moisture transfer in sand molds containing water, Metall. Trans. B, 17, 1986, p. 903-911
2. Вейник А. И, Термодинамика литейной формы, М. Машиностроение, 1968, – 335 с
3. Ле Конг Ха, Распределение влажности в сырой форме при заливке, Литейное производство, 1970, №5, c. 37-38
4. H. L. Tsai, K. C. Chiang and T. S. Chen, Movement of moisture front and alloy solidification in green sand casting. Trans. AFS, vol 96, 1986, p. 191-196
5. T. S. Shih, S. S. Siau and C. H. Hong, Movements of vaporization interface and temperature distributions in green sand molds, Trans. AFS, vol 104, 1996, p. 481-489
6. S. S. Hsiau and W. J. Chang, Cooling analysis of castings in green sand molds, Trans. AFS, vol 106, p. 595-600 
7. Савинов, А.С, Анализ силового взаимодействия литой детали с формой, Вестник МГТУ им. Г.И. Носова, 2011, №1(3), 2011
8. Kaviany, M, Principles of Heat Transfer in Porous Media, Springer-Verlag, New York, 1991
9. N. Wakao and S. Kaguei, Heat and Mass Transfer in Packed Beds, Japan, 1982
10. 10.Серебро, В.С, Основы теории газовых процессов в литейной форме, М.: Машиностроение, 1991, 208 с
11. 11. Trần Xuân Tiến, Nguyễn Hữu Miên, Đào Hồng Bách, Xác định trường ẩm và thông số nhiệt lý của khuôn cát tươi; Tạp chí Công nghệ Kim loại, số 53, 4/201