Kết quả mô phỏng cho thấy nhiệt độ được phân bố không đối xứng dọc theo đường hàn và nhiệt độ tối đa dọc theo đường hàn tăng với sự gia tăng tốc độ quay. Ngoài ra kết quả nhiệt độ ở vùng tiến lớn hơn vùng lùi.
Thermal model, simulation and experiment to determine process parameters domain in Friction stir welding of aluminum alloys
MAI ĐĂNG TUẤN3, HOÀNG TRỌNG BÁ2, ĐÀO DUY QUÍ1, TRƯƠNG MINH NHẬT1, NGUYỄN ĐĂNG MINH ĐẠT1, LƯU PHƯƠNG MINH1
(1) Trường Đại học Bách khoa Thành phố Hồ Chí Minh
(2) Trường Đại học Sư phạm kỹ thuật Thành phố Hồ Chí Minh
(3) Trường Đại học Sư phạm kỹ thuật Vĩnh Long
Liên hệ: tuanmd@vlute.edu.vn
Ngày nhận bài: 11/1/2019, Ngày duyệt đăng: 4/2/2019
TÓM TẮT
Hàn ma sát khuấy (FSW) là một trong những công nghệ hàn mới nhất, trong đó sử dụng một dụng cụ đặc biệt để tạo ra nhiệt ma sát trong phôi hàn và tạo liên kết mà không làm nóng chảy kim loại. Nói cách khác hàn ma sát khuấy là phương pháp hàn ở trạng thái rắn. Mục tiêu của bài báo là đưa ra mô hình toán về quá trình sinh nhiệt, truyền nhiệt và dòng vật liệu trong hàn ma sát khuấy. Đã sử dụng phương pháp phân tích phần tử hữu hạn (FEA) và mô phỏng trên phần mềm HyperWork để tính toán trường nhiệt độ ở trạng thái ổn định, xác định miền thông số hàn cho nhôm tấm 6061 dày 4 mm. Thí nghiệm đo nhiệt độ kiểm chứng mô hình mô phỏng được thực hiện. Mô phỏng và thực nghiệm được tiến hành với tốc độ quay và tốc độ tiến của dụng cụ thay đổi nhằm nghiên cứu sự thay đổi nhiệt độ phân bố quanh dụng cụ. Kết quả mô phỏng cho thấy nhiệt độ được phân bố không đối xứng dọc theo đường hàn và nhiệt độ tối đa dọc theo đường hàn tăng với sự gia tăng tốc độ quay. Ngoài ra kết quả nhiệt độ ở vùng tiến lớn hơn vùng lùi.
Từ khóa: Hàn ma sát khuấy, mô hình truyền nhiệt, quá trình sinh nhiệt.
ABSTRACT
Friction Stir Welding (FSW) is one of the latest welding technologies which uses a special tool to generate fric- tion heat in welding and bonding workpieces without melting the metal. In other words friction welding is a solid state welding method. The objective of this study is to provide a mathematical model of heat generation and heat transfer in friction welding. The finite element analysis (FEA) and simulation with HyperWork software are used to calculate a steady-state temperature field, this paper reports the results of statistical analysis conducted on the weld data obtained from friction stir welding of square butt-welded 4 mm thick AA6061 plate. The temperature mea- surement experiment to validate the simulation model is performed. The rotational speed and welding speed of the tool were changed to study changes in the temperature distribution around the tool. The simulation results show that the temperature is distributed asymmetric along the welding line and that the maximum temperature along the welding line increases with increasing rotation speed. In addition, the temperature at the advancing side is higher than the retreating side.
Keywords: Friction stir welding, heat transfer model, heat generation.
1. MỞ ĐẦU
Hàn ma sát khuấy là một phương pháp hàn áp lực ở trạng thái rắn được phát minh bởi Viện Hàn (TWI), Anh, năm 1991, để hàn hợp kim ở nhiệt độ thấp hơn nhiệt độ nóng chảy như hợp kim nhôm, magie, đồng (Thomas và cộng sự, 1991 [1]).
Trong hàn ma sát khuấy, một dụng cụ vừa xoay vừa tịnh tiến dọc theo đường hàn và tạo ra mối hàn thông qua sự khuấy vật liệu.
Dụng cụ hàn vừa xoay vừa tịnh tiến xuống tiếp xúc với bề mặt vật hàn nhằm tạo nguồn nhiệt cần thiết ban đầu, kế tiếp là đi xuyên vào vật hàn (chiều sâu bằng với chiều sâu ngấu) tạo những thay đổi về tổ chức vật liệu; làm cho quá trình biến dạng dẻo mãnh liệt ở vùng khuấy, sau đó di chuyển dọc theo hướng hàn tạo thành mối hàn. Nguyên lý hàn được thể hiện ở hình 1.
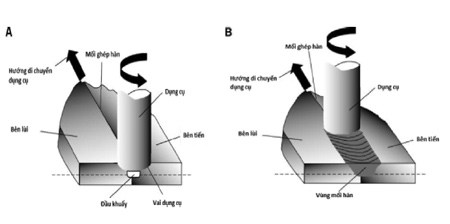
A. Đầu khuấy đi vào vật hàn, B. Di chuyển dọc đường hàn
2. THỰC NGHIỆM
a) Quá trình sinh nhiệt
Quá trình sinh nhiệt trong hàn ma sát khuấy là một quá trình chuyển đổi năng lượng cơ Pα thành nhiệt. Xét hệ số ηQ là hệ số chuyển đổi nhiệt [2], tổng lượng nhiệt sinh ra trong quá trình hàn ma sát khuấy – Qt được viết theo năng lượng tạo ra từ dụng cụ như sau:
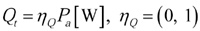
Nhiệt được sinh ra trên hoặc gần các bề mặt tương tác trên dụng cụ [2, 3, 4] và tổng lượng nhiệt sinh ra là tổng lượng nhiệt trên tất cả các bề mặt tương tác.
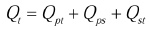
trong đó Qpt là nhiệt sinh ra tại đỉnh đầu khuấy; Qps – nhiệt sinh ra tại xung quanh đầu khuấy và Qst – lượng nhiệt sinh ra tại bề mặt của vai.
Năng lượng cơ phụ thuộc vào tốc độ góc ω và moment xoắn Mt , nên lượng nhiệt tổng sinh ra là:
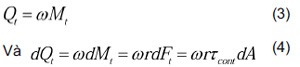
trong đó dFt là vi phân lực tác dụng, r là khoảng cách đến phân tố, dA là diện tích của phân tố, τcont là ứng suất cắt tiếp xúc trong vật liệu (Hình 2).
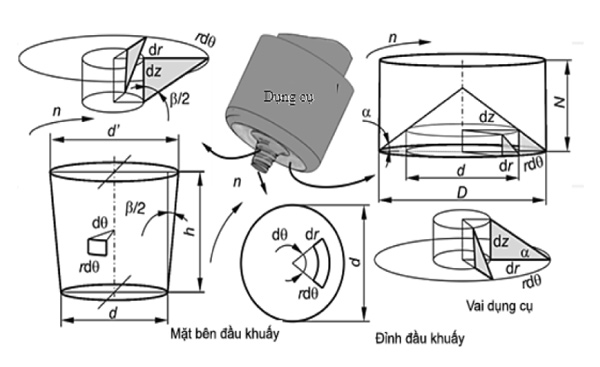
Sau khi lấy tích phân phương trình 4 biểu thức phân tích nhiệt sinh ra trên các bề mặt tương tác tương ứng là:
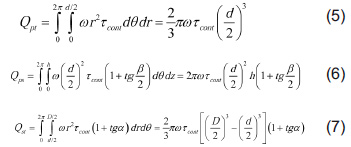
với: d là đường kính danh nghĩa của đầu khuấy, D – đường kính của dụng cụ, h – chiều cao của đầu khuấy; α – góc côn của vai hàn và β – góc côn của đầu khuấy.
b) Mô hình truyền nhiệt
Nhiệt tạo thành trong hàn ma sát khuấy bị chi phối bởi 2 cơ chế chính. Một là do ma sát và hai là do biến dạng dẻo, với nhiệt được truyền vào phôi theo định luật truyền nhiệt Fourier. Với hệ tọa độ di chuyển theo hướng di chuyển của dụng cụ y dương:
trong đó ρ, Cp, và k lần lượt là khối lượng riêng, nhiệt dung riêng và hệ số dẫn nhiệt có hướng của phôi, ⋅Q là tốc độ sinh nhiệt, VT tốc độ tiến của dụng cụ. Biểu thức điều kiện ban đầu cho việc tính toán là:
Với Ti là nhiệt độ môi trường tại thời điểm t = 0, mô hình các mặt biên tương tác giữa trong miền tính toán được thể hiện ở Hình 3. Biểu thức điều kiện biên là:
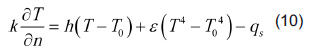
trong đó n là vectơ pháp tuyến của các mặt biên, h là hệ số đối lưu, qs là dòng nhiệt sinh ra giữa dụng cụ và phôi, ε là hệ số phát xạ và σ là hằng số Stefan – Boltzmann. Số hạng thứ 2 bên vế phải của phương trình 10 chỉ lượng nhiệt mất mát do đối lưu.
Trong phân tích truyền nhiệt tại trạng thái ổn định, có thể hiệu chỉnh sự truyền nhiệt tức thời bằng cách thiết lập trường nhiệt độ không đổi độc lập với vị trí của dụng cụ. Thực tế là, nguồn nhiệt hàn là một nguồn nhiệt di chuyển với vận tốc không đổi VT theo phương y, khi đó hệ tọa độ di chuyển (x, ξ, z):
trong đó ξ là khoảng cách từ nguồn nhiệt đến vị trí tham chiếu, tại thời điểm t và VTt là khoảng cách giữa nguồn nhiệt và gốc tọa độ tuyệt đối (x, y, z) theo phương y. Và ξ là hàm theo thời gian, và có thể viết như sau:
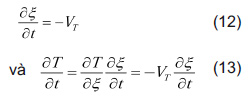
Suy ra, phương trình truyền nhiệt tức thời có thể được điều chỉnh trong hệ trục tọa độ di chuyển là:
c) Mô hình dòng vật liệu
Tính chất của vật liệu, điều kiện tải và các thông số quá trình sử dụng trong hàn ma sát khuấy đều quyết định đến bản chất của dòng vật liệu mà từ đó có thể giả thuyết rằng dòng vật liệu có tính chất đàn dẻo, dẻo hoàn toàn, dẻo nhớt hay nhớt hoàn toàn. Phương trình bảo toàn động lượng và khối lượng ở trạng thái tức thời được biểu diễn ở dạng vectơ [6] như sau:
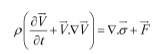và
với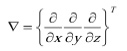 
là toán tử gradient, V→ = {u v w} T là vận tốc dòng kim loại, σ→ là tensor ứng suất tổng, ρ là khối lượng riêng của vật liệu, F→ là vector lực toàn phần, và t là biến thời gian. Tensor ứng suất tổng trong phương trình (16) được biễu diễn theo định luật Stoke [7]:
với P là áp lực thủy tĩnh, µ là độ nhớt của vật liệu và I→ là ma trận đơn vị. Từ phương trình 15, cùng với các hiệu chỉnh phù hợp do dụng cụ di chuyển, phương trình bảo toàn động lượng có thể viết thành:
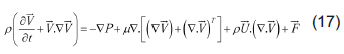
với U→ là vectơ vận tốc của dụng cụ tương đương với VT theo hướng di chuyển của dụng cụ theo phương y. Phương trình điều khiển tổng quát về sự truyền nhiệt trong hệ tọa độ Descartes sẽ là:
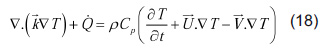
với k→ là nhiệt dẫn suất có hướng, V→ là dòng nhiệt đối lưu của dòng kim loại.
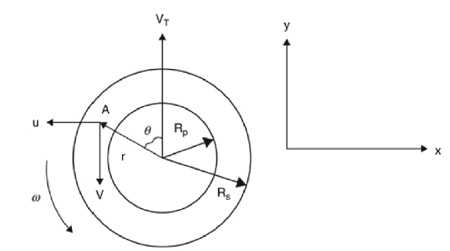
Hình 4 mô tả sơ đồ điều kiện biên vận tốc tương ứng với một dụng cụ vai phẳng và bề mặt phôi. Giả sử một điểm ‘A’ trên phôi ở bán kính r và một góc θ so sới phương của vận tốc hàn (vận tốc tiến dụng cụ) VT. Vật liệu được quay ở một tốc độ quay ω. Các thành phần vận tốc tuyến tính trên biên của bề mặt trên của vai dụng cụ được biểu diễn như sau:
Vận tốc tại chu vi của đầu khuấy là:
Điều kiện biên vận tốc tại bề mặt đỉnh đầu khuấy là:
v = ω r sin θ – VT; u = ω r cos θ, 0 ≤ r ≤ RP (21)
Với Rs, Rp và Hp lần lượt là bán kính của vai, bán kính đầu khấy và chiều cao đầu khuấy của dụng cụ dạng trụ. Nếu bỏ qua chuyển động tiến của dụng cụ, tức là dụng cụ đứng yên, thì khi đó điều kiện biên ở trên trở thành: VT = 0.
Thông lượng nhiệt biên khi phân tích trạng thái đứng yên hay ổn định hoàn toàn được biểu diễn như sau:
qs = Φ[ δωrτy (T) + (1 – ∂)ωrτf ] (22)
với τy(T) là ứng suất giới hạn chảy cắt phụ thuộc vào nhiệt độ của vật liệu tại bề mặt tiếp xúc và Φ là hệ số công suất (lượng năng lượng cơ chuyển thành nhiệt). Ứng suất tiếp ma sát τf trong phương trình 23 tương đương với áp lực tác dụng ở vai:
τf = μf PT (23)
với PT là áp lực ép lên vai và µf là hệ số ma sát giữa vai và phôi. Trong quá trình hàn, biểu thức thực nghiệm hệ số ma sát là:
μf = 0.5 X exp(-δωr) (24)
Giả sử ứng suất cắt ma sát bằng ứng suất cắt nhớt tại bề mặt tiếp xúc trong điều kiện ổn định thì:
Với các ứng suất nhớt τx, τy lấy tại biên tiếp xúc và điều kiện biên vận tốc quay được xác định trên mặt phẳng x-y và dòng theo phương z được bỏ qua. Dòng vật liệu nhớt phi Newton có thể được biểu diễn bởi mô hình độ nhớt theo nhiệt độ và tốc độ biến dạng. Khi đó ứng suất cắt là:
với µeff là độ nhớt hiệu dụng phụ thuộc vào nhiệt độ và tốc độ biến dạng, γ⋅ là tốc độ biến dạng cắt. Độ nhớt hiệu dụng được tính bởi:
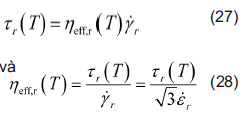
d) Mô phỏng quá trình hàn ma sát khuấy
Mô phỏng quá trình hàn ma sát khuấy bằng phần mềm HyperWork.
Công cụ mô phỏng Altair® HyperWorks® được sử dụng để mô phỏng và phân tích phần tử hữu hạn quá trình ma sát khuấy. Phương pháp phân tích hữu hạn tức thời được thực hiện bằng cách giả sử nguồn nhiệt của toàn bộ quá trình ở trạng thái ổn định.
Kết quả mô phỏng trường nhiệt độ
Các giá trị đầu vào mô phỏng gồm tốc độ quay trong khoảng 700 – 1500 v/ph và tốc độ hàn từ 0,8 đến 4 mm/s, sử dụng dụng cụ dạng trụ trơn và góc nghiêng dụng cụ là 1 đến 3o.
Kết quả mô phỏng trên hợp kim nhôm 6061 cho thấy nhiệt độ cao nhất xung quanh tâm hàn từ 300 đến 550 oC so với nhiệt độ đường rắn của nhôm 6061 là 580 oC (các hình 5, 6, và 7).
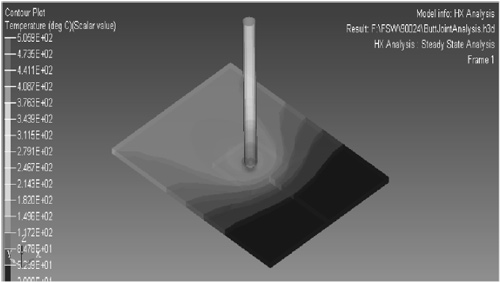
3. KẾT QUẢ VÀ THẢO LUẬN
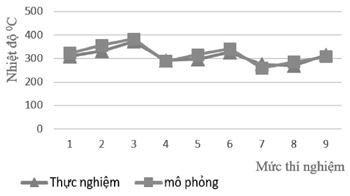
Kết quả nhiệt độ mô phỏng được kiểm chứng qua kết quả đo nhiệt độ bề mặt bằng máy đo hồng ngoại (Hình 8). Nhiệt độ được đo trên bề mặt tại biên sau của vai nhằm đo được nhiệt độ bề mặt cao nhất. Máy đo nhiệt độ hồng ngoại ghi lại nhiệt độ tại biên sau của vai trong suốt quá trình hàn sử dụng các thông số hàn tối ưu. Kết quả được thể hiện trong biểu đồ hình 9.
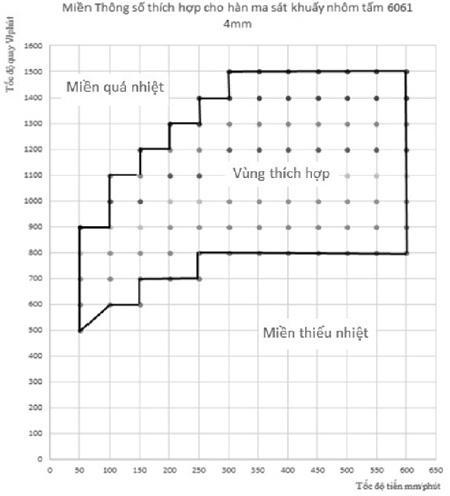
Trên cơ sở mô hình mô phỏng đã được kiểm chứng, nghiên cứu có thể đưa ra miền thông số dự đoán thích hợp cho mối hàn ma sát khuấy thực hiện trên tấm nhôm 6061 dày 4 mm (là hợp kim nhôm được sử dụng nhiều trong các ngành công nghiệp và dân dụng), bằng cách lựa chọn các cặp thông số có kết quả nhiệt độ nằm trong vùng biến dạng dẻo trạng thái rắn của nhôm 6061. Để mối hàn hình thành ở trạng thái rắn và tránh các dạng khuyết tật thì yêu cầu nhiệt độ không vượt quá nhiệt độ đường lỏng của kim loại tức là không bị quá nhiệt và không thấp hơn nhiệt độ biến dạng nóng tối thiểu tức là không bị thiếu nhiệt. Ở đây đối với nhôm 6061 thì nhiệt độ gia công biến dạng trong khoảng 430 – 580 oC [8], như vậy ta có biểu đồ miền dự đoán như trên Hình 10. Miền thông số dự đoán có xu hướng mở rộng về phía tốc độ quay và tốc độ hàn cao, tuy nhiên do giới hạn của khả năng vận hành của thiết bị nên các giá trị cao hơn sẽ không được xem xét.
Quá trình nhiệt đo được tại các giai đoạn hàn có chút khác biệt do sự khác nhau về điều kiện tản nhiệt. Ở giai đoạn đầu, phôi được gia nhiệt ma sát từ nhiệt độ môi trường, và nhiệt truyền ra mọi phương trên nền vật liệu lớn, phần mép đầu mối hàn tiếp xúc với không khí và xảy ra đối lưu. Giai đoạn giữa, mặc dù phôi đã được gia nhiệt ở giai đoạn đầu và nhiệt được tích vào dụng cụ, tuy nhiêt tại vị trí này sự truyền nhiệt xảy ra mạnh mẽ do dẫn nhiệt vào dụng cụ kẹp và hệ thống đồ gá, nên nhiệt độ ghi lại ở giai đoạn này có thấp hơn không đáng kể so với giai đoạn đầu. Cuối đường hàn, điều kiện tản nhiệt tương tự giai đoạn đầu, duy chỉ có dụng cụ đã nóng lên nhiều nên nhiệt độ lên cao hơn.
4. KẾT LUẬN
Kết quả mô phỏng số bằng phần mềm HyperWork tương đối phù hợp với dữ liệu thực nghiệm về nhiệt độ bề mặt cao nhất trên mối hàn với từng điều kiện hàn khác nhau.
Mô hình cơ nhiệt được xây dựng trên cơ sở giải quyết bài toán truyền nhiệt trong phôi hàn sau đó sử dụng kết quả trường nhiệt độ để tính ứng suất và biến dạng theo mô hình vật liệu rắn dẻo – nhớt Zener – Holoman. Nguồn nhiệt trong mô hình tính toán tạo thành do ma sát và biến dạng tại bề mặt tiếp xúc giữa dụng cụ và phôi. Nhiệt sinh ra giữa vai dụng cụ và phôi được giả thiết là do điều kiện dính (lực ma sát cắt), còn hai bề mặt còn lại coi như có tiếp xúc trượt (ma sát Coulomb). Kết quả của mô phỏng gồm trường nhiệt độ ổn định phân bố trên mối hàn và xung quanh vùng hàn với dụng cụ, trường biến dạng, áp lực, ứng suất.
Biểu đồ nhiệt độ theo thời gian trong suốt quá trình hàn cho thấy độ dốc của nhánh gia nhiệt tăng chứng tỏ tốc độ sinh nhiệt tăng khi tăng tốc độ quay và tốc độ hàn. Điều này là do tăng công suất của máy và tăng áp lực tiến của dụng cụ làm cho ma sát sinh nhiệt tăng.
Nhiệt độ cao nhất thu được tại mỗi vị trí ở thời điểm dụng cụ đã vượt qua khỏi vị trí đo, điều này hợp lý khi kết quả mô phỏng cho thấy miền nhiệt độ mở rộng ở phía sau dụng cụ do chuyển động tiến của dụng cụ.
TÀI LIỆU TRÍCH DẪN
[1]. W. M.Thomas; Friction stir butt welding. US Patent no.5460, No. 317, USA, 1991.
[2]. M .Mijajlović; Investigation and Development of Analytical Model for Estimation of Amount of Heat Generated During FSW (in Serbian), Ph. D. thesis, Faculty of Mechanical Engineering Nis, University of Nis, Nis, Serbia, 2012.
[3]. H. Schmidt and J. Hattel; An analytical model for the heat generation in friction stir welding, Modelling and Simulation in Materials Science and Engineering, Vol. 12, No. 1, 2004, pp.143-157.
[4]. R. Nandan, T. Deb Roy and H. K. D. H. Bhadeshia; Recent advances in friction-stir welding–Process, weld- ment structure and properties. Progress in Materials Science, Vol. 53(6), 2008, pp. 980-1023.
[5]. M. Djurdjanović, M. Mijajlović, D. Milčić, D. Stamenković; Heat Generation During Friction Stir Welding Process. Tribology in Industry, 31(1-2), 2009, pp. 8-14.
[6]. S. Bag and A.De; Computational Models for GTA and Laser Welding Processes, Germany : Lap Lambert Academic Publishing, 2013.
[7]. N. Rebelo and N. Kobayashi; A coupled analysis of visco- plastic deformation and heat transfer, Part I, Int. J. Mech. Sci. 22, 1980, pp. 699 – 705.
[8]. Rajiv S. Mishra, Murray W. Mahoney editors; Friction Stir Welding and Processing , 2007, pp. 7-35.
(Trong bài có một số ký tự không thể hiện đúng nguyên mẫu trên tạp chí mong các bạn đọc thông cảm. vd: U→ )
